測量及計算大區域土地面積的方法
進行大區域面積的測量,我們現在一般采用土地面積測量儀,測量方法簡單,并且結果滿足需要,不過假如臨時需要進行測量,手邊沒有土地面積測量儀,我們該怎么辦呢?今天就介紹一個測量及計算土地面積的方法。
目前計算測區面積是根據測區邊界點的高斯平面坐標,按公式(1)進行計算:
![]()
對于大面積區域,由于高斯投影是等角投影,投影后存在面積變形,且隨著測區距中央子午線越遠,面積變形越大。所以即使沒有測量誤差,按公式(1)求得的面積也并不是實際面積。
為了解決該問題,本文采用的方法是首先通過高斯投影反算,將高斯坐標轉換為大地坐標(地理坐標),然后選擇圓錐等面積投影的投影方法再將大地坐標轉換為平面坐標,即:
![]()
然后采用公式(1)計算區域面積。
另外,投影面高程對測區面積的計算也有很大影響,所以在實際計算中要對參考橢球長半軸a加改正數,即a′=a+h+ξ,式中h是投影面高程,ξ是投影區域高程異常值,由于ξ是一小量,通常可忽略不計。
為了得到用該方法計算出的測區面積值與測區的理論面積值間的差值,在橢球面上目前只能按公式(2)
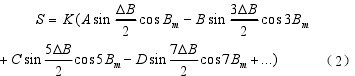
計算出規則梯形區域的理論面積值。對于不規則區域,現在還無可行的計算方法。
但在實際生產中,測區區域邊界一般都是不規則的。對于不規則的區域,無法得到其理論面積值,但可以得到一個相對不規則區域的理論面積值。其具體方法為在橢球面上選擇一個經差、緯差較大的梯形,然后在這個大的梯形四周減去一些大小不等的經差、緯差較小的梯形,減去后所得的圖形就是一個相對不規則圖形,用大梯形的理論面積值減去那些小梯形的理論面積值,就得到這個相對不規則區域的理論面積值了。其示意圖如圖1:
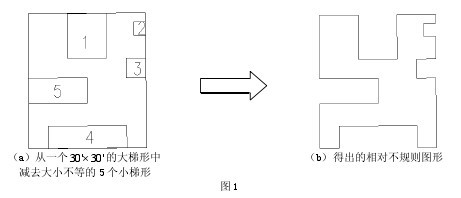
本文采用的計算圖形就是這種相對不規則圖形,通過比較分析這種相對不規則區域的理論面積值與計算值間的差值的大小,來得出一定的結論。
由于我國處于中緯度地區,所以選取梯形的緯度是位于北緯30°附近的。由于中央子午線的選取與面積的計算無關,為了便于計算,選取梯形的中央子午線的經度都是3°。又根據實際情況中可能常遇到的大區域情況,選擇了4個大小不同的相對不規則圖形來討論,分別是從10′×10′、30′×30′、40′×40′、1°×1°的大梯形中減去大小不等的小梯形得來的,其理論面積依次為215、1732、3521、8346,單位都為km2。
計算過程為先選取一個經差、緯差較大的梯形,假設該梯形的左邊線距中央子午線的經度為1°,是一個10′×10′的梯形,則該梯形四個角點的坐標依次為(4°,30°,3500)、(4°,30°10′,2000)、(4°10′,30°10′,1000)、(4°10′,30°,2700),其中高程為任意假設的大地高。通過梯形四個角的大地坐標,由式(2)算得該梯形的理論面積值,大梯形的理論面積值減去小梯形的理論面積值即得到相對不規則圖形的理論面積值。將相對不規則圖形的各拐點的大地坐標經高斯正算,得到高斯投影下的平面坐標,然后按式(1)計算,就得到由高斯投影坐標算得的面積值。將各拐點的高斯平面坐標經坐標反算,得到各點的大地坐標(因為實際情況中,測量數據一般都是直接測得的平面坐標),然后通過圓錐等面積投影再將大地坐標轉為平面坐標,再按式(1)來計算面積,即得到圓錐等面積投影下的面積值。這些計算是通過VB語言進行編程來實現的。
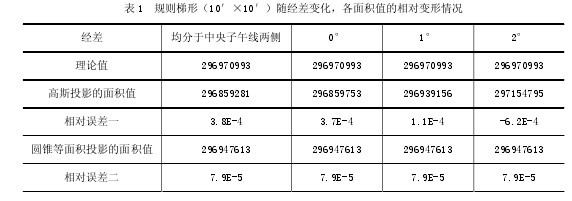
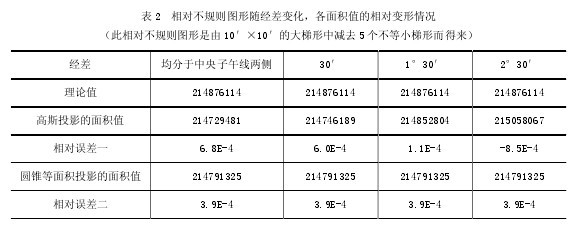
計算結果見表1、2所示,表中“經差”為梯形的左邊與中央子午線的經度差。由于面積值都較大,所以用相對誤差的大小來表示面積變形的大小。“相對誤差一”為(“理論值”-“高斯投影的面積值”)/“理論值”,“相對誤差二”為(“理論值”-“圓錐等面積投影的面積值”)/“理論值”。
表1的數據為一個規則梯形的情況,是為了與表2的相對不規則圖形作對比。從表1的數據可以看出,“相對誤差二”比“相對誤差一”低了一個數量級,且其數值不隨經差的變化而變化。說明“圓錐等面積投影的面積值”與“高斯投影的面積值”相比,變形更小,更穩定。
從表2的數據可以看出,“相對誤差二”與“相對誤差一”數量級相同,但“相對誤差二”的值不隨經差的變化而變化,其值都為3.9E-4。從30′×30′、40′×40′、1°×1°的大梯形中減去大小不等的小梯形得來的相對不規則圖形,其“相對誤差二”的數量級也與“相對誤差一”相同,但也都不隨經差的變化而變化,他們的“相對誤差二”的值分別為2.2E-4、-8.4E-5、-1.6E-3。
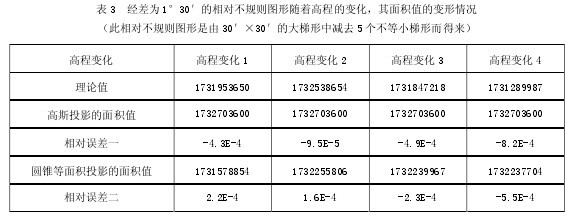
表1、表2是固定測區各拐點高程不變,從而分析測區隨著經差的變化,其面積值的變形情況。為了分析測區面積隨高程變化的情況,固定測區的經差,改變測區各拐點的高程值,其計算結果見表3所示。
從表3的數據可以看出,“相對誤差二”與“相對誤差一”的數量級基本相同,“相對誤差二”的值隨著高程的變化而變化,不過變化量不是很大。
從表1、表2、表3的數據可以得出,采用圓錐等面積投影算得的面積值與理論面積值間有一定的差值,但其并不因測區所在經差不同而不同,或因高程起伏不同,而有較大的變化,這就保證了一種相對不變性。且其計算思路簡單,可以通過編程來實現,是計算大區域土地面積的一種有效方法。




